椭圆及其标准方程
练习：
1.(多选题)已知在平面直角坐标系中,点A(-3,0),B(3,0),点P为一动点,且|PA|+|PB|=2a(a≥0),给出下列说法中正确的说法是 ( )
A.当a=2时,点P的轨迹不存在
B.当a=4时,点P的轨迹是椭圆,且焦距为3
C.当a=4时,点P的轨迹是椭圆,且焦距为6
D.当a=3时,点P的轨迹是以AB为直径的圆
2.已知椭圆过点P
和点Q
,则此椭圆的标准方程是 ( )
A.
+x2=1 B.+y2=1或x2+
=1
C.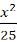
+y2=1 D.以上都不对
3.若曲线ax2+by2=1为焦点在x轴上的椭圆,则实数a,b满足 ( )
A.a2>b2 B.
<< span="">
C.0<a<b< span=""> D.0</a<b<>
4.椭圆5x2+ky2=5的一个焦点是(0,2),那么k= ( )
A.-1 B.1 C.
D.-
二、填空题(每小题5分,共10分)
5.椭圆x2+ky2=1的焦距为√2,则k= .
6.已知椭圆中心在坐标原点,焦点在x轴上,椭圆与x轴的一个交点到两焦点的距离分别为3和1,则椭圆的标准方程为 .
例1、求适合下列条件的标准方程
（1）两个焦点坐标分别是（
，0），（3，0）椭圆经过点（5，0）
（2）椭圆两焦点间的距离为16，且椭圆上某一点到两焦点的距离分别等于9和15，求椭圆的标准方程。
（3）已知椭圆的中心在原点，焦点在坐标轴上，且椭圆经过点
，
，求椭圆的方程。
解析：（1）∵ 椭圆的焦点在
轴上 ∴ 设它的标准方程为
（
）
∵ 
，
∴ 
，
∴ 
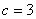
∴ 所求椭圆的方程为
（2）由题意：
，
∴ 
又焦点在
轴或
轴上 ∴ 
或
（3）∵ 椭圆的中心在原点，焦点在坐标轴上
∴ 可设椭圆的方程为
∵ 椭圆过
∴ 
∴ 
∴ 方程为
例2、方程
表示焦点在
轴上的椭圆，求实数
的取值范围。
解析：
∴ 
∴ 
例3、方程
表示何种曲线？
解析：（1）
时，
是平行于
轴的两条平行直线
（2）
时，
，方程
，表示焦点在轴上的椭圆。
（3）时，
表示圆。
（4）
时，
表示焦点在
轴上的椭圆
（5）
时，
表示平行于
轴的两条平行直线
例4、
为两个顶点坐标分别是B（0，6）和C（0，-6），另两边AB、AC的斜率的乘积是
，求顶点A的轨迹方程。
解析：设顶点A的坐标为（
） 由题意得
∴ 顶点A的轨迹方程为
（
）
例5、已知椭圆
（
），短轴的一个端点与两焦点连线构成一个正三角形且焦点到椭圆上的点的最短距离为
，求此椭圆的方程。
解析：设P为椭圆上任一点，两个焦点为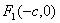
，
其中
短轴的一个端点为B（
）
∵ 
为正三角形 ∴ 
∴ 
∵ 焦点到椭圆上的点的最短距离为
∴ 
把
代入得
，
∴ 
∴ 
例6、焦点分别为（0，
）和（0，
）的椭圆截直线
所得椭圆的弦的中点的横坐标为
，求此椭圆方程。
解析：设
且
（1）
∴
∵
∴ 
∴
（2）
由（1）（2）：
，
∴ 
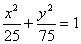
例7、P是椭圆
上的一点，F1、F2是椭圆的两个焦点，连结
、
（1）
的最小值是多少？
（2）当为钝角时，点P的横坐标取值范围是什么？
解析：（1）
（2）
∴ 
∴ 
∴ 
∴ 
例8、已知椭圆的焦点是
，P为椭圆上一点，且
是
和
的等差中项。
（1）求椭圆的方程
（2）若点P在第三象限，且
，求
解析：（1）由题设
∴ 
又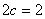
∴ 
∴ 
（2）设
，则
由正弦定理得：
∴ 
（等比定理）
∴ 
∴ 
∴ 
∴ 
∴ 
