球的体积
引入
高等于底面半径的旋转体体积对比
我们先来回忆圆面积计算公式的导出方法:
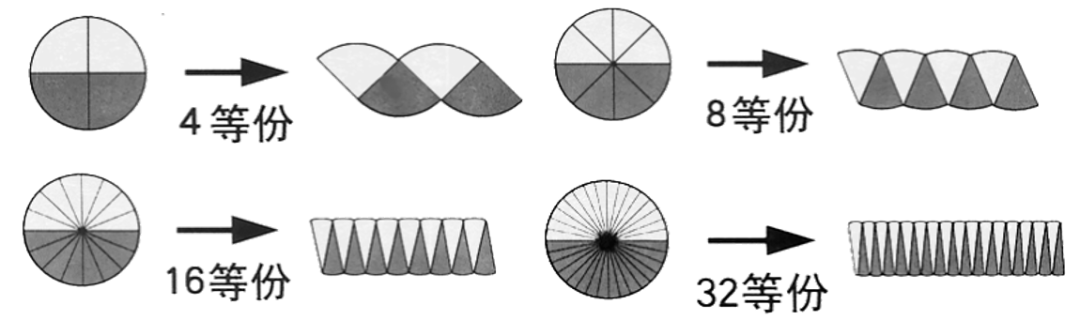
我们把一个半径为 R 的圆分成若干等分,然后如上图重新拼接起来,把一个圆近似的看成是边长分别是πR和R 的矩形.
那么圆的面积就近似等于πR^2
当所分份数不断增加时,精确程度就越来越高;当份数无穷大时,就得到了圆的面积公式。
分割
求近似和
化为准确和
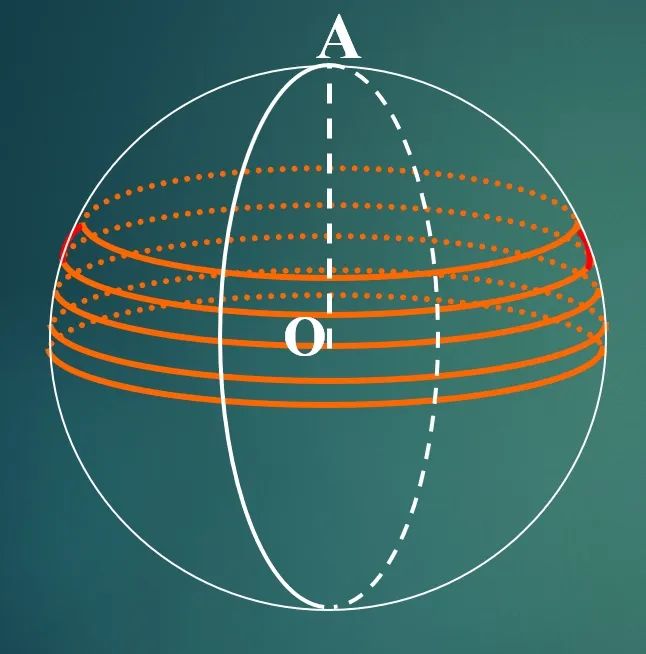
我们就运用上述方法,导出球的体积公式
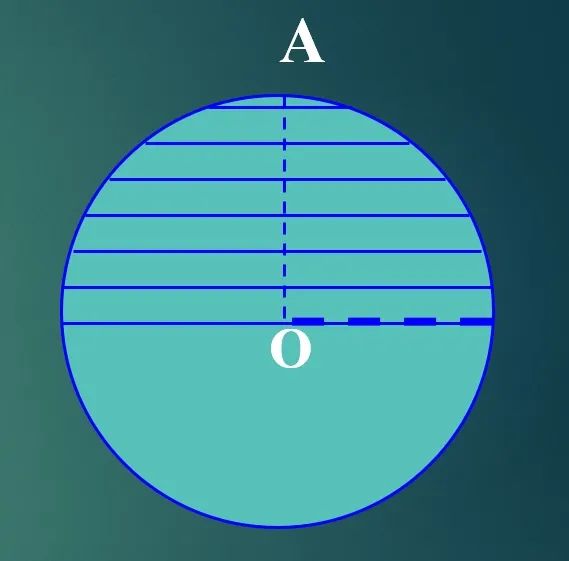
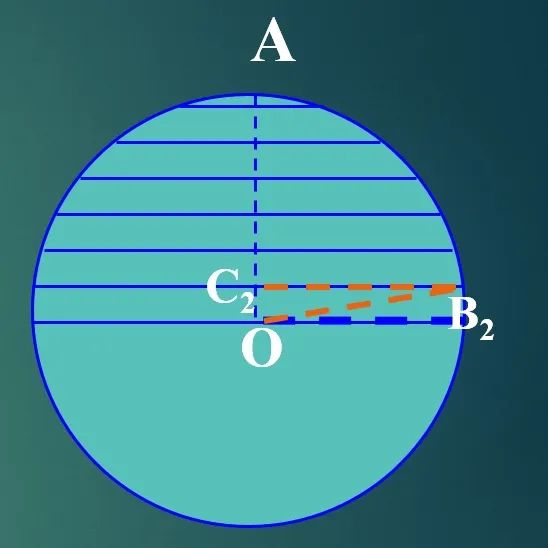
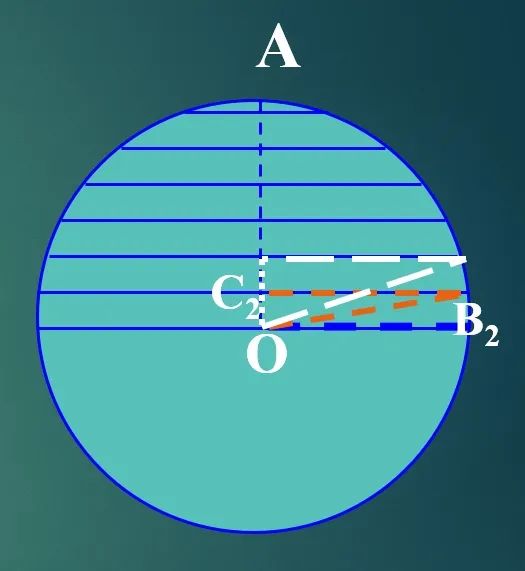
1.即先把半球分割成 、n 部分,再求出每一部分的近似体积,并将这些近似值相加,得出半球的近似体积,最后考虑 n 变为无穷大的情形,由半球的近似体积推出准确体积。
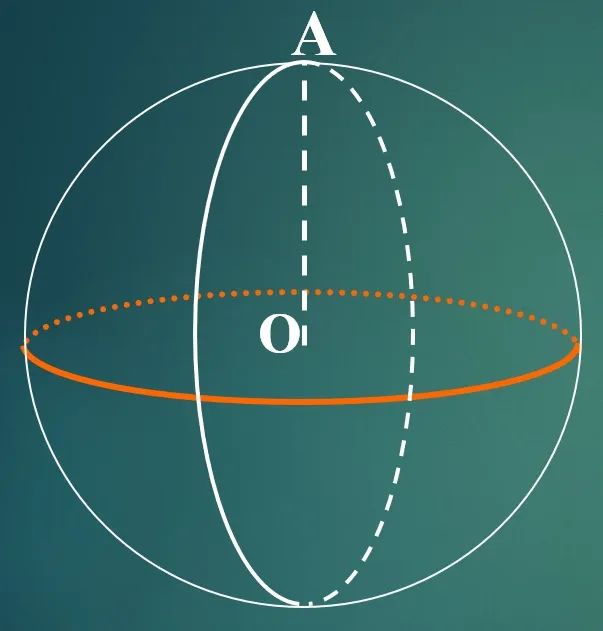



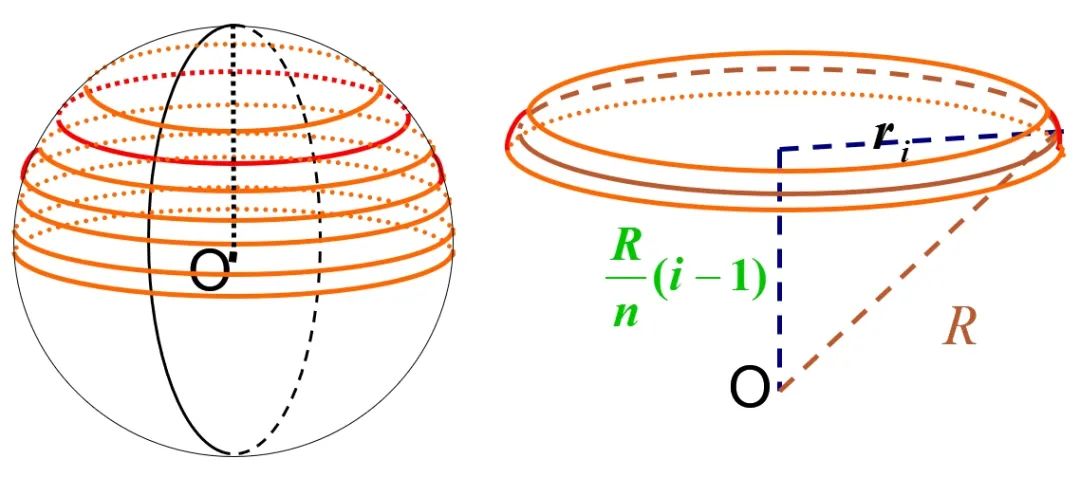
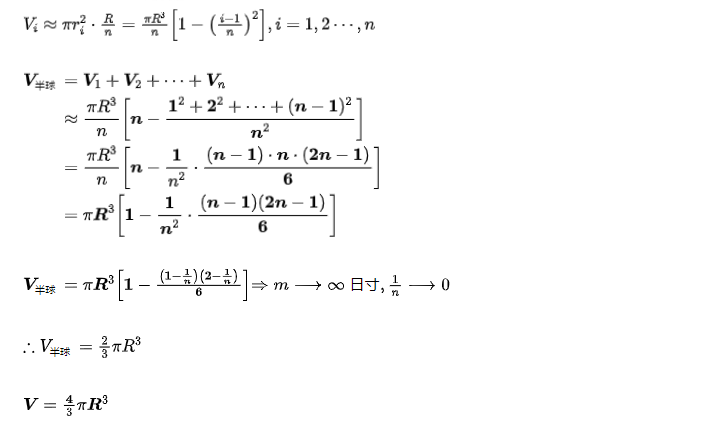
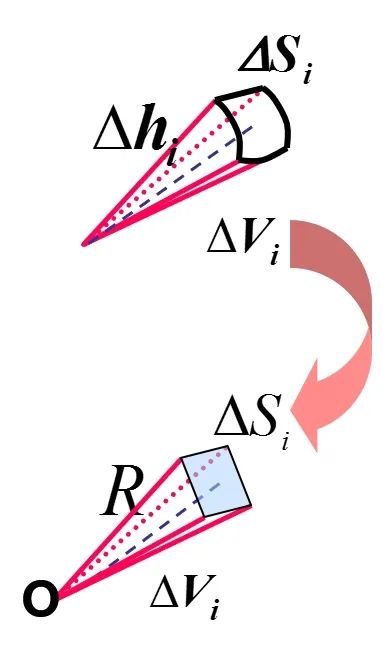
球表面积
1)球的表面是曲面,不是平面,但如果将表面平均分割成n个小块,每小块表面可近似看作一个平面,这n小块平面面积之和可近似看作球的表面积。当n
2)若每小块表面看作一个平面,将每小块平面作为底面,球心作为顶点便得到n个棱锥,这些棱锥体积之和近似为球的体积。当n

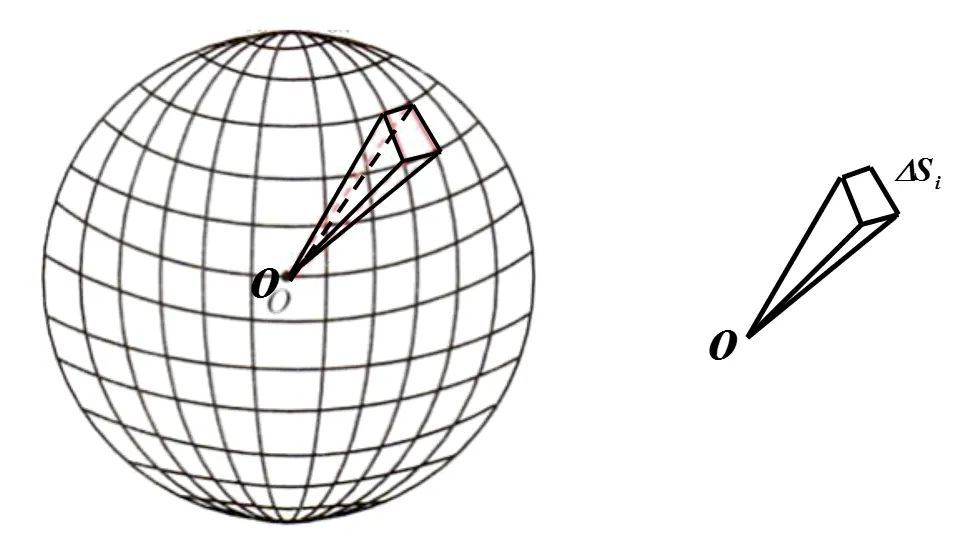
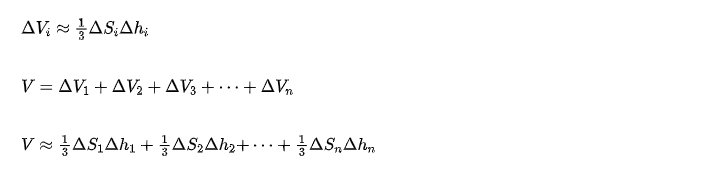

3. 如果网格分的越细,则:"小锥体"就越接近小棱锥,